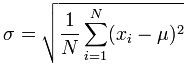Volatility

In our everyday lives, the notion of “volatility” is associated with changeability and impermanence. Whether it is applied to people’s emotions, stock market performance, political situations or the weather, being “volatile” implies a certain fickleness that seems random and capable of leading to explosive outcomes. In casino gambling, the same attributes apply.

Identifying Volatile Games

When we say a casino game is highly volatile, we mean it pays out big now and then but also causes lots of losses, making it less than reliable as a source of steady winnings. A good example is Keno with its potentially massive rewards and frequent streaks of worthless cards. Slot machines are typically very volatile, too.

On the other hand, games with a low degree of volatility are seen as more dependable, producing a rather steady dispersion of expected wins and anticipated losses. Pai Gow Poker and Baccarat come quickly to mind as table games of this sort. Roulette, Blackjack and Craps also feature limited volatility, depending on the bets that are made.

Players should be very aware of just how volatile the games they choose to play can be. Questions to ask include: How much should I expect to win (or lose) if I wager a certain amount? How likely are the outcomes of this game to fluctuate from that expectation? How confident can I be in the actual win (or loss) matching up to my predictions?

Fortunately, beyond the obvious financial swings that accompany each deal, spin or roll, there is a mathematical foundation to every game found in a casino. With a highly precise degree of predictability, it is possible to use statistical theory to calculate just exactly how volatile a game might be and use that information to one’s playing advantage.

A Matter of Standard Deviation

In gaming, the ups and downs likely to be encountered during play are characterized by a function called “Standard Deviation.” The symbol for Standard Deviation is “σ” (the lowercase Greek letter sigma). It gives us a way to know the probability of outcomes deviating from expectations, particularly in the short term. In other words, σ is how we quantify “the luck factor” in a casino game.

For any game, Standard Deviation can be determined by calculation. It is “the square root of the arithmetic mean of the squares of the deviation of each of the class frequencies from the arithmetic mean of the frequency distribution.” Expressed as an equation,

Standard Deviation Formula

where N = the number of values evaluated, x = each value in N, μ = the mean of the values and Σ is the sum of values from the first value (i = 1) to the last value (N).

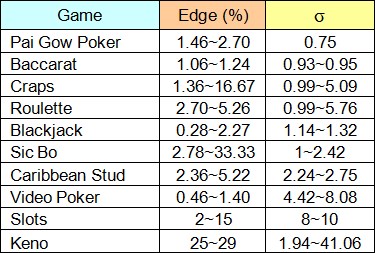
Although the math may look a bit imposing, the Standard Deviation for the most common casino games has already been worked out by gaming analysts for ready access by anyone. The following table is a simplification of the calculations expressed as ranges, taking into account varying rules and types of bets possible, and listed in order of lowest σ to highest.

Keep in mind that higher potential payouts usually mean a higher σ and thus greater volatility. Also a true picture of volatility requires comparing σ to the House Edge for the game in question. If two games have the same House Edge, the one with the higher σ will be the more volatile of the two. Similarly, if two games have the same σ, the one with the higher House Edge will be the more volatile. For a more detailed analysis of the application of Standard Deviation to casino games and bankroll management, please see the section on “Variance” provided elsewhere on this site.